文章大部分参考这里,加上自己的一点理解而已
什么是极限
构想下面一个画面:

如图所示,4.00时刻的画面由于缓冲跳过了。我们无法得知这个时刻球的位置,但是我们可以作出一个估计:
球在3:59时和4:01时球的位置之间的某个位置上
由于现实世界中球的轨迹是连续的,所以这是一个很不错的估计。
但是!如果在3:599时球突然被外星人以极快的速度吸走,在4:001时按照原来的速度和方向放回来,那么我们的估计就不正确了(尽管这不太可能发生,但是必须考虑)。
那么,如果我们把镜头放慢,慢到看得清外星人的存在,那么我们可以重新做一个更准确的估计。例如我们可以通过慢镜头,估计球在4:00的位置为“3:59.999和4:00.001的位置之间”。
假设3:59时球在9.9米处,4:01时球在10.1米处,我们可以换一种说法:
可以感性地得知,在例子中,当这个缩放级别越小时,我们便越有信心估计球的位置(如果在某个级别中发现发现球的位置发生了意外的变化,那么便很有可能要推翻10m的估计,要进一步缩小级别来确定球的位置)。
对数学极限定义的另一种理解
理解了上面的例子后,我们来看一看官方对极限的定义(official definition):
lim(x->c) f(x) = L
means for all real ε > 0 there exists a real δ > 0 such that for all x with 0 < |x − c| < δ, we have |f(x) − L| < ε (对于所有ε>0,存在一个δ > 0,使得对于所有x满足0 < |x − c| < δ,都有|f(x) − L| < ε)
可以按照以下的方式去理解:
lim(x->c) f(x) = L
//当我们充满信心地估计f(c) = L时,我们的意思是:
for all real ε > 0
//对于我们考虑所有的误差范围ε(error margin)(例如+-0.1米),
there exists a real δ > 0
//存在一个“缩放级别”δ(+-0.1秒),
such that for all x with 0 < |x − c| < δ, we have |f(x) − L| < ε
//使得估计值总是在这个误差范围内。
也就是说,如果这个估计是正确的(或者说无限有信心的),那么对于一个任意小误差范围ε,总可以找出一个缩放级别δ,令到与c距离小于δ的x(0 < |x − c| < δ),都满足f(x)的值和L之间的距离在误差范围ε内。
极限存在的必要条件是“对于任意小的误差范围总可以找到相应的缩放级别”,这个条件保证了不会漏掉“中途被外星人吸走又放回去”的情况。
也就是说:
证明极限存在
举一个例子:
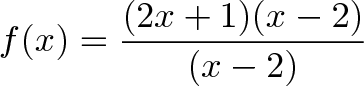
证明x=2时极限存在
我们不可以直接代入2来说明极限存在并且为5,因为(x – 2)作为分母,其值不能为0。当时当 x != 2时,我们可以将其代入,然后消掉分子和分母的(x – 2),得到f(x) = 2x + 1。
这时我们作出一个估计,当x=2时,f(x)的值为5。
我们无法得知f(2)的值,但是我们可以证明f(2)=5的估计是无限准确的。
假设允许的误差范围为+-1.0,我们有:
当x在0.5到2的区间内取值时,所有的f(x)都满足|f(x) – 5| < 1.0。
下一步我们加入error tolerance (ε) 令到这个误差区间变成任意的:
由于x – 2是单调而且连续的,所以总能找到一个x的范围,使得范围内的所有x和2的距离在+-0.5 · ε内,于是我们的估计可以无限地准确了。
函数连续(A function is continuous)
当我们说一个函数在某个区间内连续(continuous)的时候,是指它在这个区间内处处可以准确地估计,也就是:
ps:这里这是一篇通俗的传统的解释极限的文章
Can you be more specific about the content of your article? After reading it, I still have some doubts. Hope you can help me.
Glock store .com � safe, legal purchase of Glock 19s.
I don’t think the title of your article matches the content lol. Just kidding, mainly because I had some doubts after reading the article.
fusion magic mushroom bar � buy online, fast delivery, trusted source.
Lifecad � discreetly powerful carry gun.
Wonka THC chocolate bars � delicious potency, premium flavor, discreet delivery.
Beet pulp pellets price per ton � affordable, scalable for all farm sizes.
What is turbinado � natural cane sugar, less refined than white sugar.
Lifecard fegyver � Hungarian search for Lifecard pistol, same quality product.
numrich glock 19 � find Glock 19 parts from Numrich Gun Parts.